Esej na zaliczenie przedmiotu Ekonometria I -- 2012/2013

Esej powinien składać się z 4 części:

I. część makroekonomiczna -- krótki opis znaczenia wybranej kategorii makroekonomicznej na podstawie podręczników makroekonomii max 3--4 strony

II. Opis dynamiki szeregu z uwzględnieniem wahań sezonowych, wyznaczenie trendu metodą mechaniczną -- średnia ruchoma

III. Ekonometryczny model tendencji rozwojowej -- zastosować 2--3 postacie funkcji trendu (liniowa, kwadratowa, sprowadzana do liniowej), pełna diagnostyka modelu -- Mfit lub gretl.

IV. Wyznaczyć oraz porównać prognozy na 3 okresy uzyskane na podstawie: a) trendu mechanicznego b) modelu tendencji rozwojowej

Proponowana punktacja -- max 40 pkt. I. 9, II. 8 III. 15, IV. 8. Razem 40 pkt.

Uwaga: część I oraz II--IV nie muszą dotyczyć tego samego, tzn. opis kategorii nie musi dotyczyć danych wykorzystywanych w punktach II--IV.

Do analiz empirycznych proszę wykorzystać dane zawarte w pliku: https://docs.google.com/spreadsheet/ccc?key=0ApoiGfoEdPRCdG44dmt4N2prWUVybmg0ZVFVNTBMelE

Dane są w formacie Google Spreasheet. W razie problemów (których nie powinno być) proszę o kontakt.

Analiza zależności zmiennych ilościowych: regresja liniowa

Badamy jednostki statystyczne pod kątem dwóch różnych cech oznaczanych jako $X$ oraz $Y$. Symbolem $X$ oznaczamy zmienną objaśniającą (przyczynę) a symbolem $Y$ -- zmienną objaśnianą (skutek). Postulowana zależność pomiędzy $X$ oraz $Y$ może mieć różnoraki charakter. W najprostszym przypadku może to być zależność liniowa, którą można opisać równaniem: $$Y = \alpha + \beta X + \xi$$ gdzie: $Y$ --zmienna objaśniana; $X$ -- zmienna objaśniająca (w modelu bardziej ogólnym może być więcej niż jedna zmiennych objaśniających) $\alpha$, $\beta$ -- parametry; $\xi$ -- składnik losowy.

Czyni się dodatkowe założenia odnośnie rozkładu $\xi_i$ (które tutaj pominiemy).

Zadanie polega na wyznaczeniu parametrów $\alpha$, $\beta$ w oparciu o $n$-elementową próbę tj: $$y_i = \alpha + \beta x_i$$ gdzie: $y_i$ -- $i$-ta obserwacja na zmiennej objaśnianej ($i=1...n$); $x_i$ -- $i$-ta obserwacja na zmiennej objaśniającej ($i=1...n$) $\alpha$, $\beta$ -- parametry.

Zmienne $y_i$/$x_i$ mogą być szeregiem czasowym lub przekrojowym.

Metoda najmniejszych kwadratów (MNK) polega na wyznaczeniu takich ocen parametrów $\alpha$, $\beta$, aby suma kwadratów odchyleń zaobserwowanych wartości zmiennej objaśnianej ($y_i$) od jej wartości teoretycznych wyznaczonych przez funkcję regresji osiągnęła minimum. Można to zapisać: $$\Omega = \sum_{i=1}^n (y_i - (\alpha + \beta x_i))^2 \to \min$$

Rozwiązanie polega na porównaniu do zera pierwszych pochodnych cząstkowych funkcji $\Omega$ względem $\alpha$ i $\beta$ (wyprowadzenie pomijamy): $$ \begin{aligned} \hat \beta &= \frac{\sum_{i=1}^n (y_i -\bar y)(x_i - \bar x) }{ \sum_{i=1}^n (x_i - \bar x)^2 } \\ \hat \alpha &= \bar y - \bar \beta x \end{aligned} $$

Rysunek 1: Linia regresji może być lepiej lub gorzej dopasowana do danych empirycznych. Przykład dobrego dopasowania linii regresji do danych. Czerwone punkty mają współrzędne ($x_i, y_i$).

Rysunek 2: Linia regresji może być lepiej lub gorzej dopasowana do danych empirycznych. Przykład kiepskiego dopasowania linii regresji do danych. Czerwone punkty mają współrzędne ($x_i, y_i$). Wyrażenie widać, że ,,chmura punktów'' na rys. 1 zdecydowania bardziej układa się wzdłuż prostej niż na rys. 2.

Ocena jakości dopasowania linii regresji

Resztą nazywamy różnicę: $e_i = y_i - \hat y_i$, gdzie $\hat y_i = \alpha + \beta x_i $ (tzw. wartość teoretyczna zmiennej objaśnianej).

Standardowe odchylenie składnika resztowego: $$ s_{\xi} = \sqrt { \frac{1}{n-2} \sum_{i=1}^n (y_i - \hat y_i)^2 } $$ Zwane także błędem standardowym reszt. Interpretacja: ,,przeciętne odchylenie wartości teoretycznych od empirycznych zmiennej objaśnianej''.

Przykładowo dla linii regresji na rys 1 $s_{\xi}=1.21$, a na rys. 2 -- $s_{\xi}=2.77$. Jest to obiektywne i ścisłe potwierdzenie ,,wrażenia'', że jedna linia regresji jest zdecydowanie bliżej ,,chmury punktów'' niż druga. Jeżeli jednostką, w której wyrażona jest wartość $Y$ jest przykładowo hektar, to ,,przeciętne odchylenie wartości teoretycznych od empirycznych wynosi 1.21 hektara'' (dla linii regresji z rysunku 1).

Ocena przeciętnego błędu popełnianego przy szacowaniu prawdziwych wartości $\beta$ i $\alpha$. Odchylenie ocen parametrów (błąd standardowy oceny): $$ \begin{aligned} s(\beta) &= \sqrt { \frac{ s_{\xi}^2 }{\sum_{i=1}^n (x_i -\bar x)^2} } \\ s(\alpha) &= s_{\xi} \sqrt { \frac{\sum_{i=1}^n x_i^2}{n \sum (x_i -\bar x)^2} } \end{aligned} $$ Interpretacja: szacując prawdziwe wartości $\beta$ i $\alpha$ na podstawie próby losowej mylimy się przeciętnie (odpowiednio) $\pm s(\beta)$ oraz $\pm s(\alpha)$.

Przykładowo dla linii regresji z rys. 1 $s(\beta)=0.18$ a dla linii regresji z rys. 2 -- $s(\beta)=0.32$. Przeciętny błąd wynosi zatem odpowiednio około 26% wielkości ocen parametru ($s(\beta)/\beta\cdot100 \approx26$% lub $105$% ($0.32/0.303$). Kolejne potwierdzenie, że linia regresji z rys. 1 jest lepiej dopasowana.

Istotność parametrów strukturalnych ($H_0: \beta=0$). Statystyka: $$T_{n-2} = \frac{\hat \beta}{ s(\beta) } $$ ma rozkład $t$-Studenta z $n-2$ stopniami swobody. W modelu poprawnym hipoteza $H_0: \beta=0$ powinna zostać odrzucona (albo inaczej: brak podstaw do odrzucenia $H_0$ dyskwalifikuje model, bo $Y = 0 \cdot X + \alpha = \alpha$ -- zmienne $X$ i $Y$ nie są ze sobą związane)

Błąd standardowy oceny parametru $\beta$ winien być możliwie mały, i mniejszy tym lepiej. Zwróćmy uwagę, że niskim wartościom statystyki $T_{n-2}$ (co oznacza brak podstaw do odrzucenia $H_0$ -- a zatem brak podstaw do odrzucenia hipotezy o nieistotności parametru $\beta$) odpowiada sytuacja, kiedy wartość błędu standardowego oceny jest duża (względem oszacowanej wartości $\hat \beta$).

Ogólna ocena modelu -- Współczynnik zbieżności: $$ \phi^2 = \frac{\sum_{i=1}^n (y_i -\hat y_i)^2 }{ \sum_{i=1}^n (y_i -\bar y_i)^2 } \cdot 100% \quad 0\leq \phi^2 \leq 100 $$ Im $\phi^2$ jest bliższy 0, tym dopasowanie jest lepsze. Wartość $\phi^2$ interpretuje się jako ,,procent zmienności zmiennej $y$ nie objaśniony przez model regresji liniowej pomiędzy $y$ a $x$.''

Współczynnik determinacji $R^2=100-\phi^2$ interpretuje się jako ,,procent zmienności zmiennej $y$ objaśniony przez model regresji liniowej pomiędzy $y$ a $x$.''

Przykładowo dla linii regresji z rys. 1 $R^2=73$% (73% zmienności zmiennej $y$ jest objaśnione przez model regresji liniowej) a dla linii regresji z rys. 2 $R^2=46$%. Linia regresji z rys. 1 jest lepiej dopasowana.

Wyznaczenie parametrów linii regresji w arkuszu OpenOffice.org Calc

Do obliczania współczynników regresji liniowej oraz miar dopasowania w programach MS Excel oraz OpenOffice.org Calc służy polecenie REGLINP, którego składania jest następująca:

REGLINP(zakres-Y;zakres-X,1,1)

Jeżeli zmienna $x$ zapisana jest (przykładowo) w komórkach A2:A8, a zmienna $y$ w komórkach B2:B8, to wywołanie funkcji będzie miało postać:

REGLINP(B2:B8;A2:A8,1,1)

Funkcja REGLINP (w wersji OpenOffice) zwraca obszar o wielkości 5 wierszy na 2 kolumny. Poszczególne komórki tego obszaru zawierają co następuje:

$\beta$	$\alpha$
$s(\beta)$	$s(\alpha)$
$R^2$	$s_{\xi}$

Zawartość wierszy 4 i 5 nie interesuje nas....

Uwaga: funkcja REGLINP jest specjalna (bo zwraca obszar): po jej wpisaniu do komórki należy nacisnąć Ctrl-Shift-Enter a nie zwyczajne Enter.

Przykład

Przykładowy arkusz w formacie OOCalc zawiera 5 kolumn (por. tutaj: STATE -- kod stanu; TAX -- podatek od benzyny (centy/galon); INC -- dochód per capita (tysiące USD); ROAD -- długość dróg (thousands of miles of federal-aid primary highways in 1971); DLIC -- mieszkańcy stanu posiadający prawo jazdy (w procentach); FUEL -- przeciętne zużycie benzyny (gallons per person) w stanie.

Interesują nas tylko zmienne DLIC oraz FUEL.

Zależność pomiędzy przeciętnym zużyciem benzyny na mieszkańca a odsetkiem kierowców w stanie można zapisać jako: $$\mathit{FUEL} = \alpha + \beta \mathit{DLIC} + \xi$$

Oszacowana linia regresji dana jest równaniem: $$\mathit{FUEL} = 14,01 \cdot \mathit{DLIC} - 227,31$$ Zwiększenie o 1% odsetka mieszkańców posiadających prawo jazdy przeciętnie zwiększy zużycie na głowę o 14,01 galona.

Ocena dopasowania: $s_\xi=80.88$, Przeciętne odchylenie wartości teoretycznych od empirycznych wynosi 80.88 galona ($s_\xi$ jest zawsze mianowane w jednostkach zmiennej $Y$). Współczynnik zbieżności $R^2=48.9$% oznacza, że 48.9% zmienności zużycia benzyny na głowę jest objaśnione przez model regresji liniowej pomiędzy zużyciem benzyny na głowę a odsetkiem mieszkańców posiadających prawo jazdy.

Odchylenie ocen parametrów: $s(\beta)=2.13$ oraz $s(\alpha)=121.9$. Już na pierwszy rzut oka widać, że parametr $\beta$ jest istotny ($H_0: \beta=0$ należy odrzucić) ponieważ przeciętny błąd $s(\beta)$ stanowi zaledwie $15$% oceny parametru. Dokładniej: $T_{n-2} = 6.577$ (wartość krytyczna na poziomie istotności $\alpha=0.05$ dla $49-2 = 47$ stopni swobody wynosi $\approx 2.7$).

Przykładowy arkusz w formacie OOCalc jest tutaj.

Resztę proszę sobie doczytać ze slajdów....

Statystyka opisowa: dane oraz przykładowe zadania

Zaliczenia przedmiotu Statystyka opisowa

Warunkiem zaliczenia przedmiotu Statystyka opisowa jest przygotowanie w grupie maksimum 3 osób pracy, w której:

• Należy wszechstronnie porównać (średnie, rozproszenie, asymetria, wykresy) rozkład cechy dla dwóch (lub więcej) różnych zbiorowości. Można wykorzystać dane indywidualne (przykład 1 poniżej) lub pogrupowane (przykład 2), albo:

• Zamiast badania danych przekrojowych można przeprowadzić analizę dynamiki szeregu czasowego (obejmującą: średnie, różne wskaźniki dynamiki, trend+sezonowość (jeżeli występuje), wykresy), por. przykład 3.

Uwaga ważne: należy wykonać niezbędne obliczenia za pomocą arkuszy OOCalc (zalecany) lub MS Excel a opis i interpretację uzyskanych wyników zawrzeć w dokumencie w formacie OOWriter/MS Word. Opis powinien bezwzględnie zawierać stronę tytułową z tytułem pracy oraz  nazwiskami i imionami autorów.

Oba pliki (arkusz+opis) należy wysłać elektronicznie na wiadomy adres. Dodatkowo proszę o wydrukowanie i dostarczenie opisu w formie papierowej. Sam plik arkusza bez niezbędnego opisu/interpretacji nie wystarczy do uzyskania zaliczenia.

Przykładowe zadania

Przykład 1: Liczba głosów oddanych na posłów wybranych do Sejmu 7 kadencji. Porównamy dwie partie określające się jako lewicowe (cokolwiek to znaczy), tj. RP (Ruch Poparcia Palikota) oraz SLD (Sojusz Lewicy Demokratycznej)

Komentarz do obliczeń wykonanych w programie oocalc

Pobieramy dane i zapisujemy w odpowiednim formacie. Arkusz zawiera dane dotyczące wszystkich posłów. Aby oddzielić posłów RP/SLD od reszty można po prostu posortować (Dane→Sortuj) względem kolumny ,,I''. Następnie metodą kopiuj-wklej przenosimy, to co jest potrzebne do oddzielnego arkusza. Analizę przeprowadzamy oddzielnie dla posłów RP i SLD.

Przykładowy arkusz w formacie OOCalc jest tutaj.

Aby wykreślić histogram należy dane pogrupować w szereg rozdzielczy. Do tego celu służy funkcja CZĘSTOŚĆ, której składnia jest następująca:

CZĘSTOŚĆ (obszar-danych ; obszar-końców-przedziałów)

W omawianym przykładzie obszar-danych, to kolumna zawierająca liczbę oddanych na posła głosów (log). Argument obszar-końców-przedziałów to obszar górnych końców przedziałów szeregu rozdzielczego. Funkcja CZĘSTOŚĆ zwraca obszar o jedną komórkę większy od obszaru górnych końców przedziałów -- liczebność tej komórki, to liczba elementów większych od wartości ostatniego górnego końca przedziału. Krótki film ilustruje jak należy używać funkcji CZĘSTOŚĆ.

Uwaga: funkcja CZĘSTOŚĆ jest specjalna (bo zwraca obszar): po jej wpisaniu do komórki należy nacisnąć Ctrl-Shift-Enter a nie zwyczajne Enter.

Kształt histogramu (a co za tym idzie wnioski dotyczące kształtu rozkładu) zależą w dużym stopniu od sposobu pogrupowania danych w szereg rozdzielczy. Kolejny arkusz przedstawia kilka histogramów dla różnych wariantów grupowania danych.

Do obliczenia średniej, mediany, kwartyli, wariancji, odchylenia standardowego itp. służą odpowiednie funkcje. Przykładowo poniższa funkcja wyznaczy wartość mediany:

MEDIANA (obszar-danych)

Interpretacja otrzymanych wyników:

Średni liczba głosów oddanych na posła SLD wyniosła 13075 a na posła RP 14894. Jeżeli chodzi o posłów SLD to 50% zdobyło nie więcej niż 9941 głosów, 25% z nich zdobyło nie więcej niż 8041 głosów a 75% -- zdobyło nie więcej niż 15597 głosów Jeżeli chodzi o posłów RP to 50% zdobyło nie więcej niż 12828 głosów, 25% z nich zdobyło nie więcej niż 9984 głosów a 75% -- zdobyło nie więcej niż 15837 głosów Wielkości wszystkich miar średnich (oraz analiza histogramu) wskazuje, iż przeciętnie posłowie RP wybrani do Sejmu 7 kadencji zdobyli więcej głosów.

Przeciętne odchylenie liczby zdobytych głosów od średniej arytmetycznej wyniosło dla posłów SLD 9313,7 głosów a dla posłów RP 12825,5 głosów. W wartościach bezwzględnych bardziej jednorodną grupą wydają się być zatem posłowie SLD. Także wartości względne, tj. wartości współczynników zmienności (klasycznych) wynoszące odpowiednio 71,2% (SLD) oraz 90,6% (RP) wskazują na większe zróżnicowanie grupy posłów RP.

Wartości współczynników zmienności opartych o medianę i kwartyle wskazują natomiast, że zróżnicowanie liczby głosów w grupie posłów SLD ($V_q = 76%$ ) jest większe niż w grupie posłów RP ($V_q = 45%$). Podobnie wygląda wskaźnik definiowany jako $V_Q=(Q_3-Q_1)/(Q_3+Q_1)$, którego wartość dla posłów SLD wynosi 32% a dla posłów RP 22,7%.

Skąd taka dziwna wartość współczynnika $V_s$?

Obliczmy średnie i miary rozproszenia dla obu grup posłów pomijając obserwacje skrajnie nietypowe (cf. jeszcze inny arkusz). W każdej z obu grup jest jedna nietypowa obserwacja: wynik lidera listy (J. Palikot i R. Kalisz). Po usunięciu tej jednej obserwacji wszystkie współczynniki zmienności, bez wyjątku wykazują na większą zmienność grupy posłów SLD. Wniosek: miary klasyczne nie są właściwe w przypadku rozkładów zawierających wielkości nietypowe i/lub rozkładów znacznie odbiegających kształtem od rozkładu jednomodalnego.

Uwaga dla studentów: proszę obliczyć wszystkie miary a ew. zdyskwalifikować miary klasyczne jako wniosek z analizy a nie z góry założyć że miary klasyczne są do kitu i ich nie liczyć. Za takie postępowanie zostanie obniżona ocena!

Kształt rozkładów (histogram) wskazuje, że rozkłady cechuje asymetria dodatnia, przy czym asymetria w przypadku posłów SLD jest zauważalnie większa a dla posłów RP wydaje się być nieduża. Obliczone wielkości klasycznego współczynnika asymetrii ($\mu$) wskazują na ogromną asymetrię obu rozkładów ($\mu> 3$ dla SLD oraz $\mu> 5$ dla RP). Współczynniki Pearsona są znacznie niższe ($\mu = 38$ dla SLD oraz $\mu> 0,03$ dla RP) i wskazują na -- zgodną ze stanem faktycznym (wykres) sytuacją.

Wniosek: także klasyczne miary asymetrii nie są właściwe w przypadku rozkładów zawierających wielkości nietypowe i/lub rozkładów znacznie odbiegających kształtem od rozkładu jednomodalnego. Wniosek ten potwierdza analiza skośności po usunięciu wartości nietypowych (J. Palikot i R. Kalisz).

Przykład 2: porównanie struktury wieku posłów dwóch największych partii wybranych do Reichstagu w wyborach z 1930 r. (źródło cf. Młodzi, wykształceni z wielkich miast).

Obliczenia są w miarę oczywiste i nie wymagają dodatkowego komentarza. Stosowny arkusz jest tutaj.

Uwaga: analizowany szereg ma nieokreślone: dolny koniec pierwszego oraz górny koniec ostatniego przedziału. Arbitralnie przyjęliśmy 20 lat jako dolny koniec pierwszego a 80 lat jako górny koniec ostatniego przedziału. Ponieważ liczebności tych przedziałów są niewielkie ewentualny popełniony błąd także nie będzie duży.

Interpretacja otrzymanych wyników:

Średni wiek posła NSDAP wynosił 38,8 lat a posła KPD był nieco niższy bo wynosił 37,35 lat. 50% posłów NSDAP miało 37,1 lat i mniej. 25% posłów NSDAP nie było starszych niż 32,5 lat (pierwszy kwartyl, $Q_1$) a 75% nie było starszych niż 44,1 lat (trzeci kwartyl, $Q_3$). 50% posłów KPD miało 36,7 lat i mniej. 25% posłów KPD nie było starszych niż 32,4 lat a 75% nie było starszych niż 42,1 lat.

Wielkości wszystkich miar średnich (oraz analiza histogramu) wskazuje, iż przeciętnie posłowie KPD wybrani do Reichstagu w wyborach z 1930 r. byli nieco młodsi od posłów NSDAP.

Przeciętne odchylenie wieku od średniej arytmetycznej wyniosło dla posłów NSDAP 9,1 lat a dla posłów KPD 7,12 lat co wskazuje że posłowie KPD są grupą bardziej jednorodną. Potwierdzają to wartości względne, tj. wartości współczynników zmienności (klasycznych) wynoszące odpowiednio 23,5% (NSDAP) oraz 19,1% (KPD). Wartości współczynników zmienności opartych o medianę są nieco wyższe i wynoszą odpowiednio: 31,1% oraz 26,3%.

Kształt rozkładów (histogram) oraz różnica pomiędzy wielkościami miar średnich wskazuje, że rozkłady cechuje niewielka asymetria dodatnia. Co potwierdzają obliczone wielkości współczynników zarówno klasycznego ($\mu$) jak i Pearsona wykorzystującego różnice pomiędzy średnimi ($W_s$)

Przykład 3: Kwartalny skup mleka w mln litrów w Polsce w latach 1996--2003 (32 obserwacje)

Komentarz do obliczeń wykonanych w programie oocalc

Obliczenia są zawarte w arkuszu dostępnym tutaj.

Ponieważ z wykresu wynika, że mamy do czynienia z sezonowością roczną obliczamy średnią ruchomą 4-okresową (kolumna ,,D'' arkusza).

Kolumna ,,M'' zawiera obliczenia potrzebne do wyznaczenia wartości średniego błędu kwadratowego

Kolumny ,,N'' do ,,T'' zawierają obliczenia niezbędne do wyznaczenia parametrów trendu liniowego (i oceny dopasowania tegoż trendu) metodą najmniejszych kwadratów.

Kolumny ,,V'' do ,,Y'' zawierają obliczenia niezbędne do wyznaczenia wskaźników sezonowości. Wskaźniki surowe zawiera wiersz 37 a oczyszczone wiersz 40 (w kolumnach ,,V''--,,Y'')

Kolumna ,,Z'' zawiera obliczone wskaźniki sezonowości.

Skorygowane o wskaźniki sezonowości wartości funkcji trendu liniowego zawiera kolumna ,,AA''. Kolumna ,,AB'' zaś niezbędne obliczenia dla wyznaczenia RMSE (pierwiastek błędu średniokwadratowego) dla szeregu skorygowanego przez przemnożenie przez odpowiednie wskaźniki sezonowości.

Interpretacja otrzymanych wyników:

Funkcja trendu skupu mleka w Polsce w latach 1993--2003 jest następująca $$ \hat y_t = 1591849,4 + 5582,4 t $$ Z funkcji trendu wynika, że w latach 1996--2003 skup mleka w Polsce wzrastał z kwartału na kwartał średnio o 5582,4 mln litrów. Wyraz wolny funkcji trendu (1591849,4) informuje o teoretycznej wielkości skupu mleka w pierwszym kwartale 1996 r.

Odchylenie standardowe składnika losowego wynosi 258448,5 mln litrów. Średnie błędy szacunku parametrów są zaś równe $\bar \beta = 4948,3$ oraz $\bar \alpha = 93559,9$. Wielkość standardowe składnika losowego zwłaszcza w przypadku parametru $\beta$ jest znaczna co świadczy o słabym dopasowaniu do danych empirycznych. Można oczekiwać, iż test istotności parametru strukturalnego $\beta \neq 0$ wykaże iż nie ma podstaw do odrzucenia $H_0$ (sprawdzić samodzielnie!)

Słabe dopasowanie potwierdzają wielkości współczynników $\phi^2$ oraz $R^2$ wynoszące odpowiednio 96% oraz 4%, tj. 96% procent zmienności skupu mleka nie jest objaśniane przez liniową funkcję trendu. Albo: zaledwie 4% procent zmienności skupu mleka jest objaśniane przez liniową funkcję trendu.

Porównując wielkości współczynnika RMSE (pierwiastek błędu średniokwadratowego) dla liniowej funkcji trendu (RMSE_tl) oraz średniej ruchomej otrzymamy: $$ \begin{aligned} RMSE_{sr} &= \sqrt{53886700/30} =1796223.33 \\ RMSE_{tl} &= \sqrt{2003868574371/32} = 62620892949.09 \end{aligned} $$ co świadczy o dużo lepszym dopasowaniu średniej ruchomej do danych empirycznych (powodem jest oczywiście sezonowość--trend liniowy w takiej sytuacji dużo gorzej objaśnia kształtowanie się skupu mleka)

Sezonowość. Wielkość skupu mleka w pierwszym kwartale stanowiła 82,7% przeciętnej kwartalnej, zaś w drugim, trzecim i czwartym kwartale odpowiednio 110,6%, 116,9 oraz 89,8% przeciętnej kwartalnej.

Obliczenie RMSE dla danych skorygowanych dało w wyniku $232363367977,161/32 = 85213,6$ (dla danych nieskorygowanych było to $2003868574371,33/32 = 250241,7$ czyli znacznie więcej.

Dane

Pliki z przykładowymi danymi (w formacie CSV dla ułatwienia importu do różnych arkuszy i/lub innych narzędzi) oraz wyżej cytowane arkusze (w formacie OOCalc) są dostępne tutaj.

Literatura

Dokumentacja OOffice (niestety w języku).

Analiza dynamiki zjawisk

Średnia ruchoma (moving average)

Oblicznie $k$-okresowej średniej ruchomej w przypadku gdy $k$ jest liczbą nieparzystą: $$ y_{t + (k-1)/2} = \frac{1}{k} \sum_{i=t}^{t + k -1} y_i \quad t = 1,\dots,n - \frac{k-1}{2} \label{S-MovingAverage} $$

Przykładowo powyższy wzorek można rozpisać dla $k=3$ następująco: $$ \begin{aligned} \bar y_2 &= \frac{y_1 + y_2 + y_3}{3} \\ \bar y_3 &= \frac{y_2 + y_3 + y_4}{3} \\ \dots & \dots \\ \bar y_{n-1} &= \frac{y_{n-2} + y_{n-1} + y_n}{3} \end{aligned} $$

Oblicznie $k$-okresowej średniej ruchomej w przypadku gdy $k$ jest liczbą parzystą (średnia ruchoma scentrowana): $$ y_{t + k/2} = \frac{1}{k} (0,5 y_t + \sum_{i=t}^{t+k-1}y_i + 0,5 y_{t+k}) \quad t=1,\dots,n - \frac{k}{2} \label{S-MovingAverage-C} $$

Przykładowo powyższy wzorek można rozpisać dla $k=4$ następująco: $$ \begin{aligned} \bar y_3 &= \frac{0,5 y_1 + y_2 + y_3 + y_4 + 0,5 y_5}{4} \\ \bar y_4 &= \frac{0,5 y_2 + y_3 + y_4 + y_5 + 0,5 y_6}{4} \\ \dots & \dots \\ \bar y_{n-2} &= \frac{0,5 y_{n-4} + y_{n-3} + y_{n-2} + y_{n-1} + 0,5 y_n}{4} \end{aligned} $$

Ocena jakości dopasowania

Błędy prognoz ex-post

Średni błąd kwadratowy ($n^*=n -(k-1)/2$ lub $n^*=n -k/2$) w zależności od rodzaju średniej ruchomej: $$ MSE = \frac{1}{n^*} \sum_{i=1}^{n^*} (y_i -\bar y_i)^2 $$

Pierwiastek błędu średniokwadratowego: $$ RMSE = \sqrt{MSE} $$

Wykorzystanie modelu średniej ruchomej do prognozowania polega na wyznaczeniu prognozy jako średniej arytmetycznej zwykłej bądź ważonej z $k$ ostatnich wartości zmiennej, tj. $y^*_t = \frac{1}{k}\sum_{i=t-k}^{t-1}y_i$ przy czym $k$ należy wyznaczyć tak aby średni kwadratowy błąd ex post był minimalny.

Metoda analityczna

Liniowa funkcja trendu ma postać: $$y_t = \alpha + \beta t + \xi_t$$ gdzie: $y_t$ -- poziom zjawiska w okresie $t$; $\alpha$, $\beta$ -- parametry; $t$ -- zmienna czasowa (np. $t= 1,...n$) oraz $\xi_t$ -- składnik losowy.

Wartości (oceny) parametrów wyznaczone metodą najmniejszych kwadratów są następujące: $$ \begin{aligned} \hat \beta &= \frac{\sum_{t=1}^n (y_t -\bar y)(t - \bar t) }{ \sum_{i=1}^n (t - \bar t)^2 } \\ \hat \alpha &= \bar y - \bar \beta t \end{aligned} $$

Ocena jakości dopasowania

Standardowe odchylenie składnika resztowego: $$ s_{\xi} = \sqrt { \frac{1}{n-2} \sum_{t=1}^n (y_t - \hat y_t)^2 } $$

Odchylenie ocen parametrów (błąd standardowy oceny) $$ \begin{aligned} s(\beta) &= \sqrt { \frac{ s_{\xi}^2 }{\sum (t-\bar t)^2} } \\ s(\alpha) &= s_{\xi} \sqrt { \frac{\sum t^2}{n \sum (t-\bar t)^2} } \end{aligned} $$

Istotność parametrów strukturalnych ($H_0: \beta=0$). Statystyka: $$T_{n-2} = \frac{\hat \beta}{ s(\beta) } $$ ma rozkład $t$-Studenta z $n-2$ stopniami swobody.

Współczynnik zbieżności: $$ \phi^2 = \frac{\sum_{t=1}^n (y_t -\hat y_t)^2 }{ \sum_{t=1}^n (y_t -\bar y_t)^2 } \cdot 100% \quad 0\leq \phi^2 \leq 100 $$ Im $\phi^2$ jest bliższy 0, tym dopasowanie jest lepsze. Wartość $\phi^2$ interpretuje się jako ,,procent zmienności zmiennej $y$ nie objaśniony przez liniową funkcję trendu.''

Współczynnik determinacji $R^2=100-\phi^2$ interpretuje się jako ,,procent zmienności zmiennej $y$ objaśniony przez liniową funkcję trendu.''

Analiza wahań sezonowych

Zakładamy, że szereg dzieli się na $s$ powtórzeń a każde powtórzenie składa się z $k$ faz. Np. w szeregu 12 elementowym zawierającym obserwacje kwartalne $k=4$ a $s=3$.

Działania mające na celu wyodrębnienie wahań sezonowych są następujce:

Wygładzamy szereg czasowy analitycznie lub mechanicznie (średnia ruchoma).

Uwalniamy szereg czasowy od trendu. W tym celu wyliczamy wielkości $w_t = y_t/\hat y_t$

Pozbywamy się wahań przypadkowych w wielkościach $w_t$. W tym celu obliczamy średnie dla okresów jednoimiennych (surowe wskaźniki sezonowości): $$ c_i' = \frac{\sum_{j=1}^{s-1} w_{i+j\cdot k} }{s} \quad i=1, 2, \ldots ,k $$ Interpretacja: $(wskaźnik-surowy -1)\cdot 100%$ oznacza o ile procent poziom zjawiska w danej fazie jest wyższy/niższy od poziomu wyznaczonego przez trend.

Suma wskaźników surowych powinna być równa $k$, tj.  $\sum c_i'=k$. Jeżeli tak nie jest, to należy wskaźniki surowe pomnożyć przez współczynnik korygujący: $$ wk=\frac{k}{\sum c_i'} $$ Otrzymując w ten sposób czyste wskaźnik sezonowości.

Jeżeli pomnożymy w każdym okresie teoretyczny poziom zjawiska $\hat y_t$ przez odpowiedni dla danego okresu wskaźnik sezonowości, to otrzymamy teoretyczny poziom zjawiska uwzględniający wahania sezonowe.

Młodzi, wykształceni z wielkich miast

Rozkład wieku posłów Reichstagu wybranych w wyborach 1930 r.

------------------+-------+-------+------+-------+--------------
Przedział wiekowy | Razem | NSDAP | KPD* |  SPD+ | Nacjonaliści
------------------+-------+-------+------+-------+--------------
mniej niż 30      |     4 |    11 |   11 |    x  |            2
30--39            |    25 |    55 |   58 |   12  |            5
40--49            |    30 |    22 |   29 |   34  |           25
50--59            |    31 |    10 |    1 |   38  |           51
60 i więcej       |    10 |     2 |    1 |   16  |            2
------------------+-------+-------+------+-------+--------------
Razem             |   100 |   100 |  100 |  100  |          100
------------------+-------+-------+------+-------+--------------
 * komuniści + socjaldemokracji, jakby ktoś nie wiedział.

Zadanie: porównać rozkłady wieku posłów z poszczególnych partii.

Źródło: Ernest M. Doblin, Claire Pohly: The Social Composition of the Nazi Leadership, American Journal of Sociology, Vol. 51/1 (Jul 1945), pp. 42--49.

Podstawowe pojęcia statystyki opisowej

Różne pojęcia wstępne

Statystyka: analiza struktury, przedziały ufności i~weryfikacja hipotez, analiza współzależności.

Etapy analizy statystycznej: -- przełóż obserwacje na postać liczbową -- wnioskuj (zastosuj odpowiednie statystyki)

Opis statystyczny -- liczbowe przedstawienie badanych zbiorowości lub zjawisk w postaci opisu: -- tabelarycznego; -- graficznego; -- parametrycznego

Opis statystyczny może dotyczyć: -- struktury zbiorowości; -- współzależności; -- zmian zjawisk w czasie.

Badanie statystyczne to zespół czynności zmierzających do uzyskania (za pomocą metod statystycznych) informacji charakteryzujących badaną zbiorowość lub zjawisko. Najważniejsze kryteria klasyfikacji badań: -- zakres obserwacji badanych jednostek (pełne, częściowe); -- częstotliwość: (ciągłe, okresowe, doraźne); -- zasięg przestrzenny (międzynarodowe, krajowe, regionalne, środowiskowe, monograficzne); -- dziedzina badań (demograficzne, społeczne, ekonomiczne, rolnicze, jakości środowiska naturalnego itp.

Populacja, zbiorowość statystyczna: zbiór obiektów (osób, przedmiotów, zdarzeń) logicznie ze sobą powiązanych (ale nie identycznych), poddany badaniu statystycznemu.

Jednostka statystyczna: jednostki statystyczne w danej populacji różnią się od innych jednostek spoza danej populacji poprzez swoje własności wspólne (cechy stałe), jednocześnie różnią się między sobą cechami (cechy zmienne), które są przedmiotem zainteresowania badacza.

Cechy statystyczne -- właściwości jednostek statystycznych Cechy stałe -- jednakowe dla wszystkich jednostek badania: rzeczowa (co? kto? jest badane/y) przestrzenna (gdzie?) czasowa (kiedy?)

Cechy zmienne -- różnicujące jednostki, będące przedmiotem zainteresowania: -- jakościowe -- nominalne lub porządkowe -- dwudzielne lub wielodzielne -- ilościowe -- skokowe lub ciągłe

Cecha statystyczna mierzalna (ilościowa) -- określana jest za pomocą liczb np. oceny, płace. Cechy mierzalne dzielą się na skokowe i ciągłe. Skokowe są to cechy, które przyjmują skończoną liczbę wartości, zwykle są to liczby całkowite; Ciągłe są to cechy, które przyjmują dowolne wartości liczbowe z pewnego przedziału liczbowego np. dochody, długość ziarna fasoli. Cecha porządkowa.

Rodzaje skal pomiarowych -- nominalna (nominal scale), klasyfikuje: płeć; -- porządkowa (ordinal scale), klasyfikuje i porządkuje: zdolność kredytowa firmy, stadia choroby, -- Przedziałowa (interval scale), posiada jeszcze stałą jednostkę miary i umowne zero: temperatura -- Ilorazowa (rational scale), klasyfikuje, porządkuje od zera: wiek, wzrost, obrót

Pytanie: oceny w szkole to jaka skala?

Szereg rozdzielczy (punktowy, przedziałowy) -- jest to prosta tablica statystyczna złożona z dwóch kolumn lub z dwóch wierszy. W pierwszej kolumnie (wierszu) wypisujemy wartości badanej cechy, a w drugiej liczby jednostek, które mają daną cechę.

Szereg prosty powstaje poprzez uporządkowanie notowań według rosnących lub malejących poziomów cech.

Opracowanie danych

Klasyfikacja to ustalenie (wyodrębnienie) wariantów cechy.

Grupowanie -- podział zbiorowości na jednorodne lub względnie jednorodne podgrupy z punktu widzenia wyróżnionej cechy (cech): -- grupowanie typologiczne (cechy jakościowe); -- grupowanie wariancyjne (cechy ilościowe).

Zasady logiki formalnej: grupowanie musi być wyczerpujące -- każda jednostka zbiorowości musi być sklasyfikowana i włączona do odpowiedniej podgrupy; -- grupowanie powinno być rozłączne -- wyodrębnione podgrupy muszą się wzajemnie wykluczać; -- grupowanie powinno być efektywne -- wyróżnione podgrupy powinny być na tyle jednorodne jakościowo, by mogły stanowić podstawę twierdzeń uogólniających

Szeregiem statystycznym nazywamy materiał statystyczny uporządkowany lub uporządkowany i pogrupowany według określonych kryteriów (przyjętych wariantów cechy).

Szereg strukturalny:

Tablica 1. Struktura próby mieszkańców wg wykształcenia

Wykształcenie liczba osób odsetek w %
-------------------------------------
podstawowe i gimnazjalne 130  13,0
zawodowe                 272  27,2
średnie                  444  44,5
wyższe                   153  15,3
Ogółem                   999 100,0

Szereg rozdzielczy punktowy:

Struktura gospodarstw domowych wg liczby samochodów

Liczba samochodów    Liczba gospodarstw
---------------------------------------
0                      230
1                      280
2                       70
3 i więcej               5
Razem                  585

Szereg rozdzielczy przedziałowy:

Studenci według czasu wolnego

Czas wolny w min.     Liczba osób
--------------------------------
30,1 - 60                      3
60,1 - 90                      4
90,1 - 120                     6
120,1 - 150                    5
150,1 - 180                    3
180,1 - 210                    1
Razem                         22

Szereg kumulacyjny, Szereg czasowy, Szereg przestrzenny (geograficzny).

Budowa tablic statystycznych: 1. Część liczbowa (kolumny i wiersze); 2. Część opisowa: -- tytuł tablicy; -- boczek (nazwy wierszy); -- główka (nazwy kolumn); -- źródło danych; -- ewentualne uwagi odnoszące się do danych liczb.

Wykresy statystyczne są graficzną formą prezentacji materiału statystycznego, są mniej precyzyjne i szczegółowe niż tablice, natomiast bardziej sugestywne.

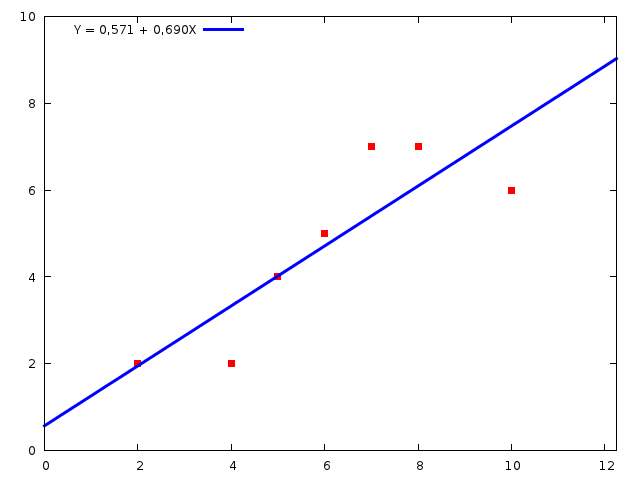
Rodzaje wykresów: -- punktowe (szereg szczegółowy, rozdzielczy punktowy, diagram korelacyjny); -- obrazkowe (szereg strukturalny, wykresy popularyzatorskie); -- powierzchniowe (prostokąty, kwadraty i koła) (rozdzielcze strukturalne, rozdzielcze przedziałowe (histogram), czasowe i przestrzenne); -- liniowe (szeregi czasowe, rozdzielcze przedziałowe (krzywa liczebności, wielobok liczebności), rozdzielcze punktowe, funkcje regresji); -- mapowe (szeregi geograficzne (kartogram lub kartodiagram)); -- złożone

Analiza struktury

Analiza struktury: badanie budowy wewnętrznej zbiorowości ze względu na obserwowane w badaniu cechy zmienne.

Podstawę do oceny struktury zbiorowości stanowią dane w postaci szeregu szczegółowego, bądź też pogrupowane

Analizę prowadzić można na podstawie wykresów, szeregów rozdzielczych oraz (najczęściej) za pomocą odpowiednio obliczonych charakterystyk, zwanych parametrami (dla populacji) lub statystykami (dla próby).

Tylko szereg rozdzielczy pokaże bezpośrednio rozkład cechy, czyli rozłożenie jednostek zbiorowości do poszczególnych wariantów badanej cechy.

Rozkład cechy: przyporządkowanie liczby wystąpień (liczebności, częstości lub prawdopodobieństwa) odpowiednim wartościom cechy zmiennej.

Analiza struktury obejmuje: określenie tendencji centralnej (wartość przeciętna, mediana, dominanta) zróżnicowanie wartości (rozproszenie) asymetrię koncentrację

Miary położenia

Klasyczne i pozycyjne. Miary przeciętne charakteryzują średni lub typowy poziom wartości cechy. Są to więc takie wartości, wokół których skupiają się wszystkie pozostałe wartości analizowanej cechy.

Do miar klasycznych zalicza się: średnią arytmetyczną

Miary pozycyjne: mediana, moda (dominanta), kwartyle, kwantyle, decyle.

Średnia arytmetyczna (Mean, Arithmetic mean): Oblicznie średniej dla szeregu prostego: $$ \bar x = \frac{\sum_{i=1}^N x_i} {N} $$

Średnia arytmetyczna ważona. Oblicznie średniej dla szeregu rodzielczego: $$ \bar x = \frac{\sum_{i=1}^k x_i n_i} {\sum_{i=1}^k n_i} $$

Mediana (Median, kwartyl drugi) dzieli zbiorowość na dwie równe części; połowa jednostek ma wartości cechy mniejsze lub równe medianie, a połowa wartości cechy równe lub większe od Me. Stąd też mediana bywa nazywana wartością środkową.

Własności mediany: -- może być obliczana w tych przypadkach, w których obliczenie średniej arytmetycznej (np. szeregi o otwartych przedziałach klasowych), a także modalnej (różne rozpiętości przedziałów klasowych) jest niemożliwe; -- mediana nie reaguje na zmiany cech skrajnych jednostek, czyli na tzw. obserwacje nietypowe (przypadkowe); -- jeżeli rozkład danych jest symetryczny, wówczas $Me = D = \bar x$.

parzysta liczba jednostek w wielkość zbiorowości: $$ \textrm{Me} = \frac{x_{n/2} + x_{n/2 +1}}{2} $$ lub (nieparzysta liczba jednostek w wielkość zbiorowości): $$ \textrm{Me} = x_{(n+1)/2} $$ lub (szereg rozdzielczy, przedziałowy): $$ \textrm{Me} = x_0 + (\frac{N}{2} - \textrm{cum}_{n-1}) \frac{c_0}{n_0} $$ gdzie: $x_0$ -- dolna granica przedziału mediany; $n_0$ -- liczebność przedziału mediany; $\textrm{cum}_{n-1}$ -- liczebność przedziału poprzedzającego przedział mediany; $c_0$ -- rozpiętość przedziału mediany.

wysokość płac  l.pracowników
800-1000       300        300
1000-1600     2400        2700
1600-2000     1200        3900
2000-3000     2500        6400
3000 i więcej 1000        7400

Dominanta (Mode, Moda, wartość modalna, wartość najczęstsza) jest to wartość cechy statystycznej, która w szeregu empirycznym występuje najczęściej. W szeregach prostych i rozdzielczych jest to wartość cechy, której odpowiada największa liczebność (częstość).

szereg rozdzielczy, przedziałowy: $$ \textrm{D} = x_0 + c_0 \frac{n_0 - n_{-1}}{(n_0 - n_{-1}) + (n_0 - n_{+1} )} $$ gdzie $x_0$ -- dolna granica przedziału najliczniejszego $n_0$ -- liczebność (gęstość) przedziału najliczniejszego $c_0$ -- rozpiętość przedziału najliczniejszego

Jeżeli przedziały mają różną rozpiętość, to można posługiwać się pojęciem gęstości.

Kwartyle ($Q$, quartile, $Q_1$, $Q_3$),

kwantyle ($D$, wartości dziesiętne),

centyle ($P$, wartości setne)

Ogólny wzór na $r$-ty centyl rzędu $r$ ($Q_{r,v}$) dla szeregu rozdzielczego wielostopniowego jest następujący $$ \textrm{Poz}_{Qr,v} = (N + 1) \frac{r}{v} \qquad \textrm{lub}\qquad \textrm{Poz}_{Qr,v} = N \frac{r}{v} $$ lub $$ Q_{r,v} = x_0 + ( \textrm{Poz}_{Qr,v} - \textrm{cum}_{n-1} ) \frac{c_0}{n_0} $$ gdzie $x_0$ -- dolna granica przedziału $Q_{r,v}$; $n_0$ -- liczebność przedziału $Q_{r,v}$; $\textrm{cum}_{n-1}$ -- liczebność przedziału poprzedzającego przedział $Q_{r,v}$; $c_0$ -- rozpiętość przedziału $Q_{r,v}$.

Miary zmienności

Wariancja, odchylenie standardowe, odchylenie przeciętne, współczynnik zmienności (Pearsona)

Wariancja (variance) jest to średnia arytmetyczna kwadratów odchyleń poszczególnych wartości cechy od średniej arytmetycznej zbiorowości.

Oblicznie wariancji dla szeregu prostego: $$ S^2 = \frac{1}{N} \sum_{i=1}^N (x_i - \bar x)^2$$ często zamiast dzielenie przez $N$ dzielimy przez $N-1$.

Oblicznie wariancji dla szeregu rodzielczego: $$ S^2 = \frac{1}{N} \sum_{i=1}^k (x_i - \bar x)^2 n_i $$ lub (prościej): $$ S^2 = \frac{1}{N} \sum_{i=1}^k x_i^2 n_i - \bar x^2 $$

Odchylenie standardowe (standard deviation, sd) jest pierwiastkiem kwadratowym z wariancji. Parametr ten określa przeciętne zróżnicowanie poszczególnych wartości cechy od średniej arytmetycznej.

Odchylenie przeciętne (average absolute deviation, $d$): $$ d = \frac{1}{N} \sum_{i=1}^n | x_i - \bar x | $$ miara bardzo rzadko używana.

Współczynniki pozycyjne. Odchylenie ćwiartkowe ($Q$, midhinge): $$ Q = \frac{Q_3 - Q_1}{2} $$ i rozstęp ćwiartkowy (interquartile range): $$ R_Q = \frac{Q_3 - Q_1}{2} $$

Współczynnik zmienności jest ilorazem bezwzględnej miary zmienności cechy i średniej wartości tej cechy. W analizie struktury korzysta się z różnych miar położenia i zmienności, dlatego są współczynniki zmienności klasyczne i pozycyjne.

Współczynniki klasyczne: $$ V_s = \frac{s}{\bar x}\qquad \textrm{lub}\qquad V_d = \frac{d}{\bar x} $$ pozycyjne $$ V_Q = \frac{Q_3 - Q_1}{\textrm{Me}} $$ albo (Quartile coefficient of dispersion): $$ V_Q = \frac{Q_3 - Q_1}{Q_3 + Q_1} $$

Współczynnik zmienności jest wartością niemianowaną. Wartości liczbowe współczynników zmienności najczęściej są podawane w procentach. Przyjmuje się, że jeżeli współczynnik zmienności jest poniżej 10%, to cechy wykazują zróżnicowanie statystycznie nieistotne. Duże wartości tego współczynnika świadczą o dużym zróżnicowaniu, a więc niejednorodności zbiorowości.

Współczynnik zmienności stosuje się zwykle w porównaniach, gdy chce się ocenić zróżnicowanie: kilku zbiorowości pod względem tej samej cechy, tej samej zbiorowości pod względem kilku różnych cech.

Momenty

Uogólniając klasyczne miary położenia i zmienności można zdefiniować następującą funkcję zwaną momentem (rzędu $r$): $$ M_r = \frac{1}{N} \sum_{i=1}^N (x_i - p)^r $$ jeżeli $p = 0$ to moment nazywamy zwykłym, jeżeli $p = \bar x$ centralnym. Momenty centralne zwykle oznacza się grecką literą $\mu$ (mju jak seria wodoszczelnych aparatów Olympusa). Momenty zwykłe są rzadziej używane (za wyjątkiem pierwszego).

Jak widać średnia to pierwszy moment zwykły a wariancja to drugi moment centralny. ,,Uproszczony'' wzór na wariancję podany wyżej sprowadza się zatem do ($m_2$ to drugi moment zwykły): $$ \mu_2 = m_2 - \mu_1^2 $$

Miary asymetrii

Asymetria (skewness), to odwrotność symetrii. Szereg jest symetryczny jeżeli jednostki są rozłożone ,,równomiernie'' wokół wartości średniej: $$ \bar x = \textrm{Me} = D $$

Asymetria prawostronna, lewostronna; wskaźnik asymetrii (skośności), współczynniki asymetrii (skośności).

Moment trzeci centralny -- średnia arytmetyczna z podniesionych do potęgi trzeciej odchyleń wartości cechy od średniej arytmetycznej $$ \mu_3 = \frac{1}{N} \sum_{i=1}^N (x_i - \bar x)^3 $$ albo (za pomocą momentów zwykłych): $$ \mu_3 = m_3 - 3 m_2 \bar x + 2 \bar x^3 $$ jeżeli $\mu_3 = 0 $ szereg symetryczny, $\mu_3 > 0 $ asymetria dodatnia (prawostronna), $\mu_3 < 0 $ asymetria ujemna (lewostronna)

Moment trzeci względny określa siłę i kierunek asymetrii: $$ g_1 = \frac{\mu_3}{s^3} $$

Na podstawie badań empirycznych: $-2 < g_1 < 2$, w skrajnych przypadkach może przekraczać ten przedział.

Współczynnik asymetrii (skośności) oparty na odległościach między średnimi (K. Pearson). $$ W_s = \frac{\bar x - D}{s} $$ rzadziej używa się: $$ W_s = \frac{\bar x - \textrm{Me}}{s} $$

Współczynnik asymetrii (skośności) oparty na odległościach między kwartylami lub decylami: $$ W_{sq} = \frac{(Q_3 - Q_2) - (Q_2 - Q_1)}{Q_3 - Q_1} $$

Miary koncentracji

Koncentracja: rozłożenie wartości cechy pomiędzy poszczególne jednostki populacji. Brak koncentracji: wszystkie jednostki mają różne wartości; maksymalna koncentracja: wszystkie jednostki mają tą samą wartość. $$ K = \frac{\mu_4}{s^4} - 3 $$ wartość K wynosi 0 dla rozkładu normalnego; jeżeli $K < 0 $ rozkład jest spłaszczony, jeżeli $K>0$ rozkład jest bardziej skoncentrowany niż rozkład normalny

Współczynnik Giniego i Krzywa Lorenza. Krzywa Lorenza jest kreślona w układzie współrzędnych $XY$. Oś $OX$ reprezentuje kumulowaną liczebność (wyrażoną najczęściej jako udział w całkowitej liczebności populacji). Oś $OY$ reprezentuje kumulowaną wartość cechy (także w %%). Każdy punkt na krzywej Lorenza reprezentuje wtedy stwierdzenie typu: 20% jednostek ma 5% łącznej wartości cechy. Np. 25% ludności posiada 8% łącznych dochodów, albo 50% rolników posiada 15% łącznych areałów, itp.

Przy założeniu, że dane są w postaci szeregu rozdzielczego a wartości kumulowane liczebności populacji oraz wartość cechy są wyrażone w %%. Współczynnik Giniego można obliczyć jako: $$ G = 1 - \left( \sum_{i=1}^k \frac{x_{cum_i} + x_{cum_{i-1}} }{2} (n_{cum_i} + n_{cum_{i-1}}) \right) / 5000 $$ przy czym $x_{cum_0} = 0 $ oraz $n_{cum_0} = 0 $; $x_{cum_i}$ -- wartość kumulowana cechy dla przedziału $i$; $n_{cum_i}$ -- wartość kumulowana liczebności dla przedziału $i$;

Powyższe to po prostu obliczenie pola pod linią łamaną w kwadracie $100 \times 100$. Połowa pola tego kwadratu wynosi 5000. Jeżeli krzywa Lorenza pokrywa się z przekątną kwadratu, to $G=0$ (brak koncentracji). Wartości większ od zera wskazują na koncentrację wartości cechy.

http://www.fao.org/ag/AGP/agpc/doc/Counprof/uruguay/uruguay.htm
------------------------------------------
           Farms Area  Farm size (hectares)
           Number       %%  Hectares    %%
-------------------------------------------
1 to 4        6,260   10.9     16,516   0.1
5 to 9        7,086   12.4     47,611   0.3
10 to 19      7,118   12.5     97,841   0.8
20 to 49      8,934   15.6    285,254   1.7
50 to 99      6,647   11.6    472,928   2.9
100 to 199    6,382   11.2    910,286   5.5
200 to 499    6,783   11.9  2,162,836  13.2
500 to 999    3,687    6.8  2,725,637  16.6
1000 to 2499  2,912    5.1  4,441,627  27.0
2500 to 4999    838    1.5  2,837,134  17.3
5000 to 9999    228    0.4  1,504,482   9.2
10000 and more   56    0.1    917,531   5.6
-------------------------------------------
TOTAL        57,131  100.0 16,419,683 100.0
-------------------------------------------

Zadanie 1:

Trasa wyścigu dookoła Flandrii liczyła w 2007 roku 259 km. Od 125 km do mety zaczęły się słynne flandryjskie pagórki, których wykaz jest na stronie http://pl.wikipedia.org/wiki/Dookoła_Flandrii_2007.

1. Wyznaczyć średnią wysokość wzniesień oraz przeprowadzić wszechstronną analizę szeregu szczegółowego wykorzystując pozycyjne miary przeciętnego poziomu (dominanta, mediana, kwartyle)

2. Przeprowadzić szczegółową analizę wykorzystując miary dyspersji i asymetrii.

3. Zbudować szereg rozdzielczy.

Szybkie wprowadzenie do programu MicroFit

Import danych z arkusza Excel poprzez schowek do programu MF

W skoroszycie MAK_KON_08 (do pobrania, przykładowo ze strony docs.google.com) arkusz opis zawiera krótkie opisy zmiennych. Jako przykład wybieramy zmienną ZPP (rys. 1).

Rysunek 1. Arkusz opis w skoroszycie MAK_KON_08

Zmienna ZPP znajduje się w arkuszu makro (rys. 2).

Rysunek 2. Arkusz makro w skoroszycie MAK_KON_08

Uwaga: Zwykle separatorem dziesiętnym w programie Excel jest przecinek, tymczasem poprawna konwersja poprzez schowek z Excela do MF wymaga ustawienia kropki jako separatora części całkowitej/ułamkowej (tzw. separator dziesiętny w Excelu).

Aby zmienić separator dziesiętny na kropkę należy (opis dotyczy Excela w wersji 2003): wybrać Opcje w menu Narzędzia, następnie usunąć ptaszka w polu Użyj separatorów systemowych, a w polu separator dziesiętny wstawić kropkę. (rys. 3 i 4.)

Rysunek 3. Ustawienie kropki jako separatora dziesiętnego w Excelu

Rysunek 4. Ustawienie kropki jako separatora dziesiętnego w Excelu (cd)

Teraz w programie Excel kopiujemy kolumnę zawierającą zmienną ZPP do schowka, przechodzimy do okna programu MF i z menu File wybieramy Input New Data from Clipboard (rys. 5).

Rysunek 5. Import przez schowek

Pojawi się okno jak na rys. 6.

Rysunek 6. Import przez schowek (cd)

Należy wybrać No dates (bo kopiujemy tylko zmienną ZPP a daty określimy później) oraz Names/Descriptions in the first row (chyba że nie skopiowaliśmy pierwszego wiersza).

Po wybraniu No dates należy określić częstotliwość danych (w naszym przykładzie dane są kwartalne, tj. Quarterly) oraz numer pierwszej obserwacji (rys. 7).

Rysunek 7. Import przez schowek (cd)

W sytuacji jak na rys. 7, naciskając przycisk OK kończymy procedurę wczytania zmiennej do MF poprzez schowek.

Uwaga: jeżeli po naciśnięciu przycisku OK, MF zgłosi błąd, to coś pokręciliśmy w procedurze powyżej i należy spróbować raz jeszcze.

Przekształcanie zmiennych

Po prawidłowym wczytaniu zmiennej ZPP program MF przechodzi do okna Process, w którym można dokonywać różnych przekształceń zmiennych.

MF nie rozróżnia w nazwach zmniennych dużych i małych liter. Zmienne opóźnione definiuje się przykładowo jako X1=X(-1), co oznacza iż X1 jest zmienną opóźnioną o jeden okres. Podobnie tworzy się zmienne z wyprzedzeniem czasowym (rys. 8).

Rysunek 8. Okno Process

Przyciski Constant oraz Time Trend pozwalają na szybkie zdefiniowanie stałej oraz trendu (zmiennej równej 1 dla pierwszej obserwacji i zawierającej kolejne liczby naturalne dla następnych obserwacji).

Stałą można także zdefiniować w oknie Command and Data transformations, wpisując przykładowo stala=1 (rys. 9).

Rysunek 9. Zdefiniowanie stałej

Po wpisaniu formuły naciskamy przycisk Run (umieszczony na prawym brzegu okna). Można wpisać wiele poleceń na raz -- wówczas należy je oddzielić średnikiem. Rysunki 10 i 11 pokazują w jaki sposób definiuje się logarytm zmiennej ZPP oraz kwadrat zmiennej TREND.

Rysunek 10. Utworzenie logarytmu zmiennej ZPP

Rysunek 11. Utworzenie kwadratu zmiennej TREND

Wpisując w oknie Command and Data transformations PLOT ZPP (i naciskając przycisk Run) spowodujemy wyświetlenie wykresu liniowego dla zmiennej ZPP (rys. 12).

Rysunek 12. Wyświetlenie wykresu -- funkcja PLOT

Trend liniowy

Naciskamy przycisk Single w menu na górze okna. W dużym białym polu tekstowym definiujemy równanie wpisując (lub wybierając z pola wyboru Variables umieszczonego na górze okna) zmienną zależną jako pierwszą; po niej nazwy zmiennych niezależnych (rys. 13).

Rysunek 13. Okno Single

Wybierając odpowiednie wartości z pól tekstowych można łatwo ustalić stosowną wielkość próby. Domyślnie wielkość próby to wszystkie obserwacje w szeregu.

Formułę trendu liniowego dla ZPP pokazuje rys. 14.

Rysunek 14. Trend liniowy dla ZPP

Po naciśnięciu ikony Run otrzymujemy wynik (rys. 15).

Rysunek 15. Trend liniowy dla ZPP (cd)

Po naciśnięciu ikony Close możemy przejść do menu analizy wyników regresji oraz menu testowania hipotez.

Trend kwadratowy i potęgowy

Formułę trendu kwardatowego dla ZPP pokazuje rys. 16.

Rysunek 16. Trend kwadratowy dla ZPP

Po naciśnięciu ikony Run otrzymujemy wynik (rys. 17).

Rysunek 17. Trend kwadratowy dla ZPP (cd)

W podobny sposób szacujemy trend potęgowy, uprzednio obliczając logarytmy zmiennych ZPP (rys. 10) oraz TREND (na rys. 18 oznaczone jako LZPP oraz LTREND).

Rysunek 18. Trend potęgowy dla ZPP

Po naciśnięciu ikony Run otrzymujemy wynik (rys. 19).

Rysunek 19. Trend potęgowy dla ZPP

Kryteria oceny pracy magisterskiej/licencjackiej

Formularz oceny pracy stosowany na WZUG zawiera sześć następujących syntetycznych kryteriów (w nawiasie maksymalna możliwa liczba punktów do uzyskania):

1. Poprawność sformułowania tematu (0--10)
2. Zgodność treści pracy z jej tematem (0--10)
3. Ocena układu pracy, struktury, podziału treści, kompletności tez (0--20)
4. Ocena merytoryczna pracy, w tym oryginalność ujęcia problemu, dobór metod i narzędzi badawczych (0--40)
5. Ocena doboru i wykorzystania źródeł (0--15)
6. Ocena formalnej strony pracy w tym przypisy, język (0--5)

Powyższe sumuje się do 100. Skala ocen jest zaś następująca: bardzo dobry (91--100); dobry plus (81--90); dobry (66--80); dostateczny plus (56--65); dostateczny (41--55); niedostateczny (do 40).

Ogólne wymagania dla przygotowania pracy licencjakiej i/lub magisterskiej

Informacje podstawowe

Wykonanie pracy licencjackiej lub magisterskiej obejmuje wykonanie określonego przez promotora eksperymentu (programistycznego, zastosowania metody lub systemu, porównania metod lub systemów, projektowania, dowodzenia twierdzenia lub innego eksperymentu) oraz przygotowanie pracy w formacie i wymaganej liczbie egzemplarzy ustalonych przez władze stosownego Wydziału/Uczelni. Wymagane jest także dostarczenie -- oprócz wersji ,,papierowej'' -- dokumentu elektronicznego (szczegółowe wymagania są różne, czasami świadczą o małych kompetencjach w/z publikowania dokumentów elektronicznych ciała je stanowiącego).

Zaleca się umieszczenie na końcu pracy następującego oświadczenia: Ja, niżej podpisany(a) oświadczam, iż przedłożona praca dyplomowa została wykonana przeze mnie samodzielnie, nie narusza praw autorskich, interesów prawnych i materialnych innych osób. Oświadczenie należy oznaczyć datą i podpisem. Proszę się upewnić/zapytać w dziekanacie o dokładne brzmienie oświadczenia.

Praca licencjacka pisemna winna obejmować ok. 30--60 stron, a praca magisterska ok. 60--90 stron maszynopisu. Winna być przygotowana formacie LaTeX (preferowany przeze mnie), Open Office, MS Word (w ostateczności) lub innym programie (wg ustalenia z promotorem), tak aby oprócz formy drukowanej promotor mógł otrzymać wersję elektroniczną.

Uwaga: Nie ma ściśle ustalonego układu graficznego określającego marginesy, krój/stopień pisma, odstępy między śródtytułami. Dopuszczalna jest zatem pewna dowolność w tym zakresie, ale podstawowe zasady obowiązują i są one następujące: format strony A4, stopień pisma nie większy niż 12pt, jako podstawowy font dokumentu należy stosować jakiś krój szeryfowy (Times New Roman, Book Antiqua, itp.; Arial tylko do tytułów) odstęp między wierszami 1,5.

Układ pracy

Praca pisemna winna mieć następujący układ:

1. Strona tytułowa winna zawierać tytuł pracy, nazwisko i imię autora, promotora, rok i miejsce złożenia pracy).

2. Spis treści.

3. Wstęp zawierający: cel, motywację, metodologię pracy, układ pracy. Uwaga: nie należy we wstępie ,,rozpoczynać pracy'', np. umieszczać tu definicje, klasyfikacje itp.

4. Część opisowa: opis wyników studium literaturowego dla tematu pracy (metody, algorytmy, systemy itp. wykorzystane w części eksperymentalnej, metody, algorytmy i systemy im pokrewne bądź alternatywne, ze wskazaniem ich wad, zalet, dziedzin zastosowań i ograniczeń), w podsumowaniu uzasadnienie eksperymentu planowanego w części doświadczalnej.

5. Część doświadczalna: hipoteza badawcza, opis planowanego eksperymentu, metody, algorytmy, narzędzia, uzasadnienie wyboru (jeśli zaczerpnięte z szeroko rozumianej literatury, ze wskazaniem na część opisową, jeśli własne, oryginalne, szczegółowy opis), przebieg eksperymentu, wyniki eksperymentu.

6. Dyskusja: ocena wiarygodności wyników, ich oryginalności, porównanie ze znanymi z literatury itp.

7. Podsumowanie/wnioski: najważniejsze osiągnięcia pracy, wynikające wnioski dla ewentualnych dalszych badań (Podsumowanie winno opierać się w całości na materiale zawartym w pracy).

8. Literatura.

9. Spis tabel i spis rysunków.

10. Ewentualny wykaz skrótów i oznaczeń stosowanych w pracy.

11. Ewentualne załączniki.

12. Ewentualny skorowidz (skorowidze).

Termin ,,eksperyment'' należy rozumieć szeroko, stosownie do tematu pracy. Przykładowo eksperymentem może być:

1. Implementacja systemu lub programu komputerowego (hipotezą badawczą jest wtedy specyfikacja systemu, opis wyniku obejmuje m.in. instrukcję obsługi programu, przykłady użycia);

2. Porównanie systemów komputerowych/metod programowania czy projektowania/algorytmów itp. (hipoteza badawcza: przewaga jednego nad drugim);

3. Zastosowanie systemu komputerowego lub algorytmu do rozwiązania zadania praktycznego (hipoteza badawcza: system nadaje się do rozwiązania określonego zadania).

Spis literatury

W spisie literatury należy umieszczać tylko te pozycje, które są cytowane w pracy.

Spis literatury należy przygotować w układzie alfabetycznym. Nie należy dzielić wykazu na kategorie, np. książki, artykuły, dokumenty internetowe. Pomijając wszystkie inne czynniki, wykaz literatury dla pracy mgr/lic jest tak krótki, że nie ma to większego sensu.

Pozycje literaturowe w spisie literatury można oznaczać: liczbą umieszczoną w nawiasie kwadratowym (zalecane), np. [3], umieszczonym w nawiasie okrągłym nazwiskiem autora i rokiem wydania, np.: (Cacacki, 1994) przy czym jeżeli w tym samym roku (pierwszy) autor ma więcej publikacji, to oznaczamy pozycje kolejno literkami, np. (Cacacki, 2000b).

Podając pozycję bibliograficzną należy podać: nazwisko autora, inicjał imienia, tytuł pracy, nazwę wydawcy, rok wydania. Jeżeli jest to czasopismo, należy podać dodatkowo: nazwę czasopisma, numer tomu, numery stron. Nie podaje się w tym przypadku nazwy wydawcy. Jeżeli jest to fragment książki (lub materiały z konferencji), to podajemy dodatkowo: tytuł książki, ew. nazwisko i inicjał redaktora oraz numery stron. Jeżeli jest to cytat z dokumentu dostępnego w Internecie, to podajemy dodatkowo adres WWW. Można nie podawać w tym przypadku nazwy wydawcy. Błędem jest umieszczenie wyłącznie adresu WWW w spisie literatury, bez określenia autora i tytułu dokumentu. Proszę się wzorować na poniższych przykładach:

Pozycje literatury cytuje się tak, jak się je oznacza, z tym, że pozycje oznaczone w spisie za pomocą liczby cytuje się w nawiasie kwadratowym, np. [13]. Jeżeli cytujemy wiele prac na raz odpowiednie numery należy umieścić w nawiasie kwadratowym i oddzielić przecinkami, np. [3,7,24]. W przypadku cytowania za pomocą nazwiska autora/roku postępujemy podobnie: (Cacacki 1980), (Cacacki 1992, Dadacki 1990).

Przykłady (Odpowiednio: książka, artykuł, fragment książki, dokument internetowy, praca zbiorowa typu encyklopedycznego):

[1] Knuth D. E., The TeXbook, Addison-Wesley 1986.

[2] Shave M. J. R., ,,Entities, functions and binary relations: steps to conceptual schema'', The Computer Journal 1981, 24/1.

[3] Jones M. L., ,,On the development of Data Models'', w: Edwards L. P. (red.), On the Conceptual Modelling, Berlin, Springer-Verlag 1984, s. 113--118.

[4] Pepper S., Whirlwind Guide to SGML Tools and Vendors, http://www.infotek.no/sgmltool/index.htm.

[22] Rocznik demograficzny 2000, GUS, Warszawa, 2001.

[24] Rocznik statystyczny Polski 2005, GUS, Warszawa, 2006.

Uwaga: numery pozycji niekoniecznie muszą być wewnątrz nawiasów kwadratowych -- może być bez nawiasów z kropką.

Jeżeli w pracy do cytowania wykorzystuje się schemat autor/rok, powyższy przykładowy spis winien wyglądać następująco:

Knuth D. E. (1986), The TeXbook, Addison-Wesley.

Shave M. J. R. (1981), ,,Entities, functions and binary relations: steps to conceptual schema'', The Computer Journal 24/1.

Jones M. L. (1984), ,,On the development of Data Models'', w: Edwards L. P. (red.), On the Conceptual Modelling, Berlin, Springer-Verlag, s. 113--118.

Pepper S., Whirlwind Guide to SGML Tools and Vendors, http://www.infotek.no/sgmltool/index.htm.

Rocznik demograficzny 2000 (2001), GUS, Warszawa.

Rocznik statystyczny Polski 2005 (2006), GUS, Warszawa.

Uwaga: Jeżeli do cytowania nie używamy numerów, nie należy ich umieszczać w spisie (bo w tym przypadku są tylko bezużytecznymi ozdobnikami).

Na podobnej zasadzie co prace zbiorowe typu encyklopedycznego (słowniki, roczniki statystyczne, encyklopedie) proponuję potraktować Wikipedię.

Machine learning, Wikipedia, http://en.wikipedia.org/wiki/Machine_learning.

Problem z wpisami z Wikipedii jest taki, że trudno ustalić datę ich wydania oraz autorów. Proponuję zatem pomijać datę wydania. Wpisy typu Wiki demonstrują też, że najmniej kłopotliwym system cytowania jest poprzez numer pracy ze spisu literatury.

Przygotowanie spisu literatury w systemie LaTeX można zautomatyzować wykorzystując program Bibtex. Użytkownicy OpenOffice mogą spróbować system bibus. Zaletą korzystania z programów do zarządzania jest możliwość korzystania z gotowej informacji bibliograficznej, udostępnionej on-line (np. jako usługa Scholar firmy Google).

Uwagi różne

Uwaga: porządek poniższych uwag jest dowolny; w szczególności nie odzwierciedla on ich istotności (ważne i mniej ważne są przemieszane).

Wszystkie rysunki i tabele w pracy muszą być numerowane i opatrzone tytułem/opisem. Zaleca się umieszczanie tytułu tabeli nad tabelą a opis rysunku pod rysunkiem. Tabele/rysunki muszą być opisane w tekście pracy; opis musi zawierać odsyłacz do tabeli/rysunku. Przykład opisu:

Szczegóły przedstawiono na rysunku 4, ...
Rys. 12 przedstawia rozszerzony model TAM

Albo

Model TTF (por. rys. 11) zawiera siedem następujących czynników...

Odsyłacze typu ,,tabela poniżej'', ,,powyższy rysunek'' są niedopuszczalne -- zawsze należy używać numeru.

Rysunki/tabele umieszcza się bezpośrednio w tekście, w miejscu pierwszego wzmiankowania. Jeżeli rysunek/tabela jest zbyt duży, może zostać przesunięty na początek następnej strony. Tabele mogą być dzieleone między strony, ale należy traktować to jako ostateczność (lepiej przesunąć tabelę na początek następnej strony niż podzielić między stronice--to jest powód, dla którego nie wolno używać odnośników powyżej/poniżej).

W przypadku rysunków/tabel należy określić ich autorstwo (źródło), podając je w podpisie rysunku lub tytule tabeli. Zamiast w podpisie można określić źródło w osobnym wierszu umieszczonym na dole tabeli/rysunku. Przykład (źródło w tytule tabeli):

Model TAM (źródło: [nr-pozycji-literaturowej])

Zamiast numeru oczywiście należy użyć innego schematu cytowania literatury, jeżeli takowy obowiązuje w pracy. Rysunki/tabele zaprojektowane samodzielnie oznaczamy frazą ,,opracowanie własne'', np.:

Model XTAM (źródło: opracowanie własne)

Nie używamy zwrotów Tabela nr. 99, rysunek nr. 5, tylko Tabela 99, rysunek 5.

Na końcu tytułów/śródtytułów, tytułów tabel i rysunków oraz pagin nie umieszcza się kropki.

Unikać eufemizmów/makaronizmów. Lista nielubianych/nadużywanych wyrazów zawiera m.in.: profesjonalny, biznesowy, elastyczny. Przykładowo profesjonalny (system, program), w znaczeniu będący na wysokim poziomie w danej dziedzinie zastąpić należy konkretem (lub konkretami). Podobnie w pozostałych przypadkach.

Unikać zwrotów: obecnie, wkrótce, powszechnie, itp... przy opisywaniu jakiegoś zjawiska. Należy (prawie) zawsze określać precyzyjnie co-gdzie-kiedy, oraz -- w miarę możliwości -- podać źródło danych.

Zaleca się wykorzystanie formy bezosobowej, np. przedstawiono, ustalono, omówiono, w czasie przeszłym. Nie należy mieszać stylów narracji, posługujemy się w całej pracy jednym najlepiej wykorzystującym formę bezosobową.

Nie używamy niepotrzebnie zaimków, w tym--a zwłaszcza, zaimków dzierżawczych (mój, twój, nasz, wasz, ich, jego, jej). Zamiast nasz system, nasz program lepiej często po prostu: system, program ewentualnie system X.

Podając definicje i klasyfikacje pojęć obowiązkowo wskazujemy źródło (chyba, że sami jesteśmy autorami). Przykłady:

Informacja to jest przyrost wiedzy, który może być uzyskany na podstawie danych (Tstchizris i Lochovsky 1965)...
Turski [34] definiuje Informatykę jako naukę o przetwarzaniu informacji zwłaszcza przy użyciu automatycznych środków pomocniczych...
Hurtownia danych to (por. Immon 1995): zbiór danych wspomagający podejmowanie decyzji, uporządkowany tematycznie, zintegrowany, zawierający wymiar czasowy oraz nieulotny.

Nie podaje się źródeł dla pojęć ,,oczywistych'', tj. ogólnie znanych: przykładowo nie podajemy źródeł definicji bitu, średniej arytmetycznej, itp.

Typowa praca składa się z 3--4 rozdziałów, podzielonych na punkty i ewentualnie podpunkty. Nie należy stosować bardziej szczegółowego podziału pracy. Tytuły wszystkich części pracy muszą być numerowane. Zwyczajowo natomiast Wstęp, Zakończenie, Spis Literatury i Skorowidz nie są numerowane.