Import danych z arkusza Excel poprzez schowek do programu MF
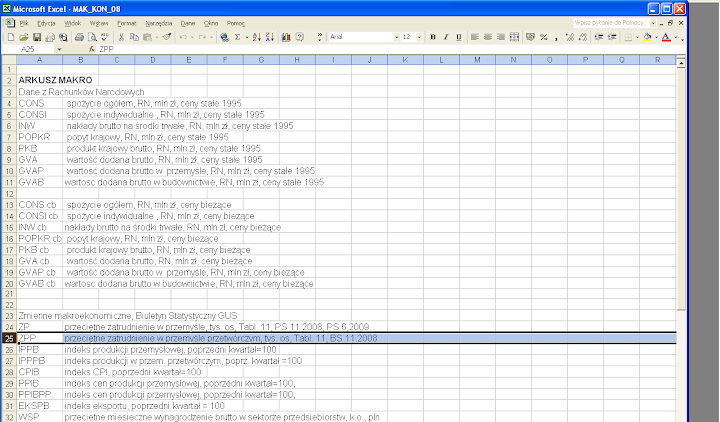
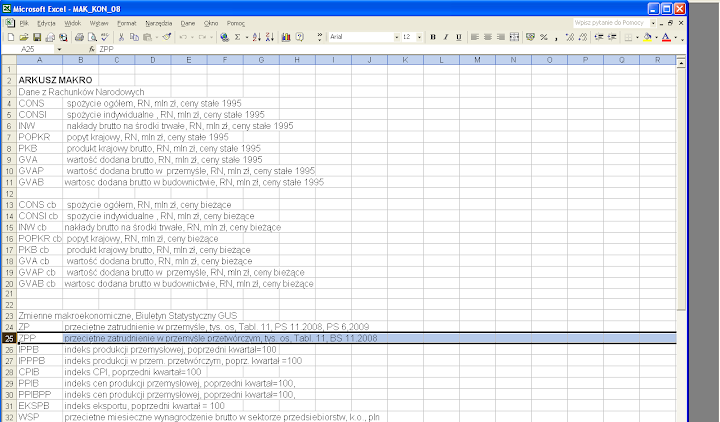
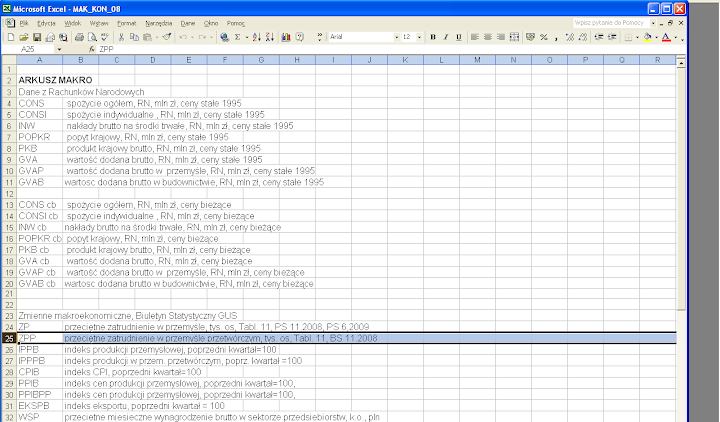
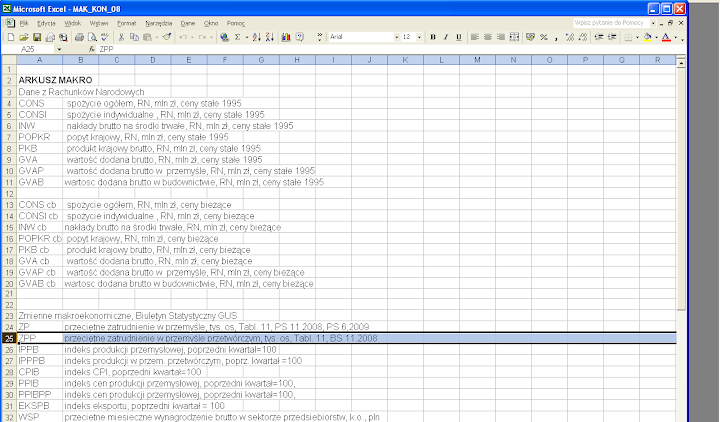
W skoroszycie MAK_KON_08 (do pobrania, przykładowo ze strony docs.google.com) arkusz opis zawiera krótkie opisy zmiennych. Jako przykład wybieramy zmienną ZPP (rys. 1).
Rysunek 1. Arkusz opis w skoroszycie MAK_KON_08

Zmienna ZPP znajduje się w arkuszu makro (rys. 2).
Rysunek 2. Arkusz makro w skoroszycie MAK_KON_08

Uwaga: Zwykle separatorem dziesiętnym w programie Excel jest przecinek, tymczasem poprawna konwersja poprzez schowek z Excela do MF wymaga ustawienia kropki jako separatora części całkowitej/ułamkowej (tzw. separator dziesiętny w Excelu).
Aby zmienić separator dziesiętny na kropkę należy (opis dotyczy Excela w wersji 2003): wybrać Opcje w menu Narzędzia, następnie usunąć ptaszka w polu Użyj separatorów systemowych, a w polu separator dziesiętny wstawić kropkę. (rys. 3 i 4.)
Rysunek 3. Ustawienie kropki jako separatora dziesiętnego w Excelu

Rysunek 4. Ustawienie kropki jako separatora dziesiętnego w Excelu (cd)

Teraz w programie Excel kopiujemy kolumnę zawierającą zmienną ZPP do schowka, przechodzimy do okna programu MF i z menu File wybieramy Input New Data from Clipboard (rys. 5).
Rysunek 5. Import przez schowek
Pojawi się okno jak na rys. 6.
Rysunek 6. Import przez schowek (cd)

Należy wybrać No dates (bo kopiujemy tylko zmienną ZPP a daty określimy później) oraz Names/Descriptions in the first row (chyba że nie skopiowaliśmy pierwszego wiersza).
Po wybraniu No dates należy określić częstotliwość danych (w naszym przykładzie dane są kwartalne, tj. Quarterly) oraz numer pierwszej obserwacji (rys. 7).
Rysunek 7. Import przez schowek (cd)

W sytuacji jak na rys. 7, naciskając przycisk OK kończymy procedurę wczytania zmiennej do MF poprzez schowek.
Uwaga: jeżeli po naciśnięciu przycisku OK, MF zgłosi błąd, to coś pokręciliśmy w procedurze powyżej i należy spróbować raz jeszcze.
Przekształcanie zmiennych
Po prawidłowym wczytaniu zmiennej ZPP program MF przechodzi do okna Process, w którym można dokonywać różnych przekształceń zmiennych.
MF nie rozróżnia w nazwach zmniennych dużych i małych liter. Zmienne opóźnione definiuje się przykładowo jako X1=X(-1), co oznacza iż X1 jest zmienną opóźnioną o jeden okres. Podobnie tworzy się zmienne z wyprzedzeniem czasowym (rys. 8).
Rysunek 8. Okno Process

Przyciski Constant oraz Time Trend pozwalają na szybkie zdefiniowanie stałej oraz trendu (zmiennej równej 1 dla pierwszej obserwacji i zawierającej kolejne liczby naturalne dla następnych obserwacji).
Stałą można także zdefiniować w oknie Command and Data transformations, wpisując przykładowo stala=1 (rys. 9).
Rysunek 9. Zdefiniowanie stałej

Po wpisaniu formuły naciskamy przycisk Run (umieszczony na prawym brzegu okna). Można wpisać wiele poleceń na raz -- wówczas należy je oddzielić średnikiem. Rysunki 10 i 11 pokazują w jaki sposób definiuje się logarytm zmiennej ZPP oraz kwadrat zmiennej TREND.
Rysunek 10. Utworzenie logarytmu zmiennej ZPP
Rysunek 11. Utworzenie kwadratu zmiennej TREND

Wpisując w oknie Command and Data transformations PLOT ZPP (i naciskając przycisk Run) spowodujemy wyświetlenie wykresu liniowego dla zmiennej ZPP (rys. 12).
Rysunek 12. Wyświetlenie wykresu -- funkcja PLOT

Trend liniowy
Naciskamy przycisk Single w menu na górze okna. W dużym białym polu tekstowym definiujemy równanie wpisując (lub wybierając z pola wyboru Variables umieszczonego na górze okna) zmienną zależną jako pierwszą; po niej nazwy zmiennych niezależnych (rys. 13).
Wybierając odpowiednie wartości z pól tekstowych można łatwo ustalić stosowną wielkość próby. Domyślnie wielkość próby to wszystkie obserwacje w szeregu.
Formułę trendu liniowego dla ZPP pokazuje rys. 14.
Rysunek 14. Trend liniowy dla ZPP

Po naciśnięciu ikony Run otrzymujemy wynik (rys. 15).
Rysunek 15. Trend liniowy dla ZPP (cd)

Po naciśnięciu ikony Close możemy przejść do menu analizy wyników regresji oraz menu testowania hipotez.
Trend kwadratowy i potęgowy
Formułę trendu kwardatowego dla ZPP pokazuje rys. 16.
Rysunek 16. Trend kwadratowy dla ZPP

Po naciśnięciu ikony Run otrzymujemy wynik (rys. 17).
Rysunek 17. Trend kwadratowy dla ZPP (cd)
W podobny sposób szacujemy trend potęgowy, uprzednio obliczając logarytmy zmiennych ZPP (rys. 10) oraz TREND (na rys. 18 oznaczone jako LZPP oraz LTREND).
Rysunek 18. Trend potęgowy dla ZPP
Po naciśnięciu ikony Run otrzymujemy wynik (rys. 19).
Rysunek 19. Trend potęgowy dla ZPP

