Badamy jednostki statystyczne pod kątem dwóch różnych cech oznaczanych jako $X$ oraz $Y$. Symbolem $X$ oznaczamy zmienną objaśniającą (przyczynę) a symbolem $Y$ -- zmienną objaśnianą (skutek). Postulowana zależność pomiędzy $X$ oraz $Y$ może mieć różnoraki charakter. W najprostszym przypadku może to być zależność liniowa, którą można opisać równaniem: $$Y = \alpha + \beta X + \xi$$ gdzie: $Y$ --zmienna objaśniana; $X$ -- zmienna objaśniająca (w modelu bardziej ogólnym może być więcej niż jedna zmiennych objaśniających) $\alpha$, $\beta$ -- parametry; $\xi$ -- składnik losowy.
Czyni się dodatkowe założenia odnośnie rozkładu $\xi_i$ (które tutaj pominiemy).
Zadanie polega na wyznaczeniu parametrów $\alpha$, $\beta$ w oparciu o $n$-elementową próbę tj: $$y_i = \alpha + \beta x_i$$ gdzie: $y_i$ -- $i$-ta obserwacja na zmiennej objaśnianej ($i=1...n$); $x_i$ -- $i$-ta obserwacja na zmiennej objaśniającej ($i=1...n$) $\alpha$, $\beta$ -- parametry.
Zmienne $y_i$/$x_i$ mogą być szeregiem czasowym lub przekrojowym.
Metoda najmniejszych kwadratów (MNK) polega na wyznaczeniu takich ocen parametrów $\alpha$, $\beta$, aby suma kwadratów odchyleń zaobserwowanych wartości zmiennej objaśnianej ($y_i$) od jej wartości teoretycznych wyznaczonych przez funkcję regresji osiągnęła minimum. Można to zapisać: $$\Omega = \sum_{i=1}^n (y_i - (\alpha + \beta x_i))^2 \to \min$$
Rozwiązanie polega na porównaniu do zera pierwszych pochodnych cząstkowych funkcji $\Omega$ względem $\alpha$ i $\beta$ (wyprowadzenie pomijamy): $$ \begin{aligned} \hat \beta &= \frac{\sum_{i=1}^n (y_i -\bar y)(x_i - \bar x) }{ \sum_{i=1}^n (x_i - \bar x)^2 } \\ \hat \alpha &= \bar y - \bar \beta x \end{aligned} $$
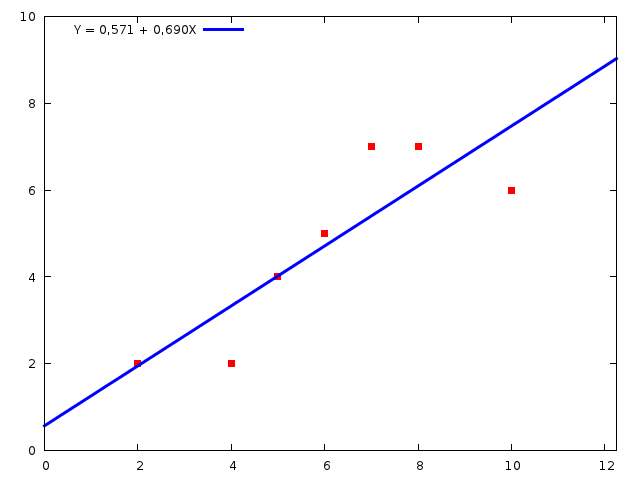
Rysunek 1: Linia regresji może być lepiej lub gorzej dopasowana do danych empirycznych. Przykład dobrego dopasowania linii regresji do danych. Czerwone punkty mają współrzędne ($x_i, y_i$).

Rysunek 2: Linia regresji może być lepiej lub gorzej dopasowana do danych empirycznych. Przykład kiepskiego dopasowania linii regresji do danych. Czerwone punkty mają współrzędne ($x_i, y_i$). Wyrażenie widać, że ,,chmura punktów'' na rys. 1 zdecydowania bardziej układa się wzdłuż prostej niż na rys. 2.
Ocena jakości dopasowania linii regresji
Resztą nazywamy różnicę: $e_i = y_i - \hat y_i$, gdzie $\hat y_i = \alpha + \beta x_i $ (tzw. wartość teoretyczna zmiennej objaśnianej).
Standardowe odchylenie składnika resztowego: $$ s_{\xi} = \sqrt { \frac{1}{n-2} \sum_{i=1}^n (y_i - \hat y_i)^2 } $$ Zwane także błędem standardowym reszt. Interpretacja: ,,przeciętne odchylenie wartości teoretycznych od empirycznych zmiennej objaśnianej''.
Przykładowo dla linii regresji na rys 1 $s_{\xi}=1.21$, a na rys. 2 -- $s_{\xi}=2.77$. Jest to obiektywne i ścisłe potwierdzenie ,,wrażenia'', że jedna linia regresji jest zdecydowanie bliżej ,,chmury punktów'' niż druga. Jeżeli jednostką, w której wyrażona jest wartość $Y$ jest przykładowo hektar, to ,,przeciętne odchylenie wartości teoretycznych od empirycznych wynosi 1.21 hektara'' (dla linii regresji z rysunku 1).
Ocena przeciętnego błędu popełnianego przy szacowaniu prawdziwych wartości $\beta$ i $\alpha$. Odchylenie ocen parametrów (błąd standardowy oceny): $$ \begin{aligned} s(\beta) &= \sqrt { \frac{ s_{\xi}^2 }{\sum_{i=1}^n (x_i -\bar x)^2} } \\ s(\alpha) &= s_{\xi} \sqrt { \frac{\sum_{i=1}^n x_i^2}{n \sum (x_i -\bar x)^2} } \end{aligned} $$ Interpretacja: szacując prawdziwe wartości $\beta$ i $\alpha$ na podstawie próby losowej mylimy się przeciętnie (odpowiednio) $\pm s(\beta)$ oraz $\pm s(\alpha)$.
Przykładowo dla linii regresji z rys. 1 $s(\beta)=0.18$ a dla linii regresji z rys. 2 -- $s(\beta)=0.32$. Przeciętny błąd wynosi zatem odpowiednio około 26% wielkości ocen parametru ($s(\beta)/\beta\cdot100 \approx26$% lub $105$% ($0.32/0.303$). Kolejne potwierdzenie, że linia regresji z rys. 1 jest lepiej dopasowana.
Istotność parametrów strukturalnych ($H_0: \beta=0$). Statystyka: $$T_{n-2} = \frac{\hat \beta}{ s(\beta) } $$ ma rozkład $t$-Studenta z $n-2$ stopniami swobody. W modelu poprawnym hipoteza $H_0: \beta=0$ powinna zostać odrzucona (albo inaczej: brak podstaw do odrzucenia $H_0$ dyskwalifikuje model, bo $Y = 0 \cdot X + \alpha = \alpha$ -- zmienne $X$ i $Y$ nie są ze sobą związane)
Błąd standardowy oceny parametru $\beta$ winien być możliwie mały, i mniejszy tym lepiej. Zwróćmy uwagę, że niskim wartościom statystyki $T_{n-2}$ (co oznacza brak podstaw do odrzucenia $H_0$ -- a zatem brak podstaw do odrzucenia hipotezy o nieistotności parametru $\beta$) odpowiada sytuacja, kiedy wartość błędu standardowego oceny jest duża (względem oszacowanej wartości $\hat \beta$).
Ogólna ocena modelu -- Współczynnik zbieżności: $$ \phi^2 = \frac{\sum_{i=1}^n (y_i -\hat y_i)^2 }{ \sum_{i=1}^n (y_i -\bar y_i)^2 } \cdot 100% \quad 0\leq \phi^2 \leq 100 $$ Im $\phi^2$ jest bliższy 0, tym dopasowanie jest lepsze. Wartość $\phi^2$ interpretuje się jako ,,procent zmienności zmiennej $y$ nie objaśniony przez model regresji liniowej pomiędzy $y$ a $x$.''
Współczynnik determinacji $R^2=100-\phi^2$ interpretuje się jako ,,procent zmienności zmiennej $y$ objaśniony przez model regresji liniowej pomiędzy $y$ a $x$.''
Przykładowo dla linii regresji z rys. 1 $R^2=73$% (73% zmienności zmiennej $y$ jest objaśnione przez model regresji liniowej) a dla linii regresji z rys. 2 $R^2=46$%. Linia regresji z rys. 1 jest lepiej dopasowana.
Wyznaczenie parametrów linii regresji w arkuszu OpenOffice.org Calc
Do obliczania współczynników regresji liniowej oraz miar dopasowania w programach MS Excel oraz OpenOffice.org Calc służy polecenie REGLINP, którego składania jest następująca:
REGLINP(zakres-Y;zakres-X,1,1)
Jeżeli zmienna $x$ zapisana jest (przykładowo) w komórkach A2:A8, a zmienna $y$ w komórkach B2:B8, to wywołanie funkcji będzie miało postać:
REGLINP(B2:B8;A2:A8,1,1)
Funkcja REGLINP (w wersji OpenOffice) zwraca obszar o wielkości 5 wierszy na 2 kolumny. Poszczególne komórki tego obszaru zawierają co następuje:
| $\beta$ | $\alpha$ |
| $s(\beta)$ | $s(\alpha)$ |
| $R^2$ | $s_{\xi}$ |
Zawartość wierszy 4 i 5 nie interesuje nas....
Uwaga: funkcja REGLINP jest specjalna (bo zwraca obszar): po jej wpisaniu do komórki należy nacisnąć Ctrl-Shift-Enter a nie zwyczajne Enter.
Przykład
Przykładowy arkusz w formacie OOCalc zawiera 5 kolumn (por. tutaj: STATE -- kod stanu; TAX -- podatek od benzyny (centy/galon); INC -- dochód per capita (tysiące USD); ROAD -- długość dróg (thousands of miles of federal-aid primary highways in 1971); DLIC -- mieszkańcy stanu posiadający prawo jazdy (w procentach); FUEL -- przeciętne zużycie benzyny (gallons per person) w stanie.
Interesują nas tylko zmienne DLIC oraz FUEL.
Zależność pomiędzy przeciętnym zużyciem benzyny na mieszkańca a odsetkiem kierowców w stanie można zapisać jako: $$\mathit{FUEL} = \alpha + \beta \mathit{DLIC} + \xi$$
Oszacowana linia regresji dana jest równaniem: $$\mathit{FUEL} = 14,01 \cdot \mathit{DLIC} - 227,31$$ Zwiększenie o 1% odsetka mieszkańców posiadających prawo jazdy przeciętnie zwiększy zużycie na głowę o 14,01 galona.
Ocena dopasowania: $s_\xi=80.88$, Przeciętne odchylenie wartości teoretycznych od empirycznych wynosi 80.88 galona ($s_\xi$ jest zawsze mianowane w jednostkach zmiennej $Y$). Współczynnik zbieżności $R^2=48.9$% oznacza, że 48.9% zmienności zużycia benzyny na głowę jest objaśnione przez model regresji liniowej pomiędzy zużyciem benzyny na głowę a odsetkiem mieszkańców posiadających prawo jazdy.
Odchylenie ocen parametrów: $s(\beta)=2.13$ oraz $s(\alpha)=121.9$. Już na pierwszy rzut oka widać, że parametr $\beta$ jest istotny ($H_0: \beta=0$ należy odrzucić) ponieważ przeciętny błąd $s(\beta)$ stanowi zaledwie $15$% oceny parametru. Dokładniej: $T_{n-2} = 6.577$ (wartość krytyczna na poziomie istotności $\alpha=0.05$ dla $49-2 = 47$ stopni swobody wynosi $\approx 2.7$).
Przykładowy arkusz w formacie OOCalc jest tutaj.
Resztę proszę sobie doczytać ze slajdów....